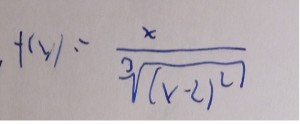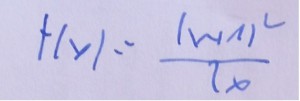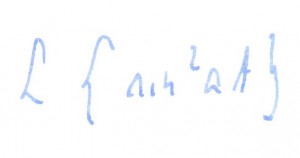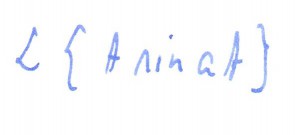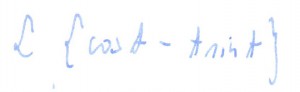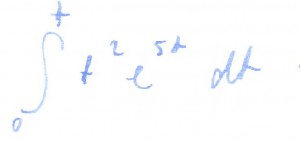Obliczyć:
Rozwiązać równanie:
Wyznaczyć obrazy danych wzorów przy wskazanym odwzorowaniu:
Obliczyć:
Obliczyć:
Wyznaczyć odwzorowanie zbioru D w funkcji omega:
Obliczyć:
Znaleźć:
Znaleźć:
udowodnij:
Dla jakich liczb zespolonych funkcja przyjmuje tylko wartości rzeczywiste ujemne:
Oblicz wartość podanej funkcji trygonometrycznej:
Oblicz wartość podanej funkcji trygonometrycznej:
Oblicz wartość podanej funkcji trygonometrycznej:
Oblicz wartość podanej funkcji trygonometrycznej:
Udowodnij:
Udowodnij:
Udowodnij:
Udowodnij:
Obliczyć logarytm z liczby zespolonej:
Obliczyć logarytm z liczby zespolonej:
Obliczyć logarytm z liczby zespolonej:
Obliczyć logarytm z liczby zespolonej:
Obliczyć logarytm z liczby zespolonej:
Oblicz wartość podanej funkcji trygonometrycznej:
Oblicz wartość podanej funkcji trygonometrycznej:
wyznaczyć liczbę zespoloną z spełniającą warunek:
wyznacz część rzeczywistą i część urojoną funkcji:
wyznacz część rzeczywistą i część urojoną funkcji:
wyznacz część rzeczywistą i część urojoną funkcji:
wyznacz część rzeczywistą i część urojoną funkcji:
wyznacz część rzeczywistą i część urojoną funkcji:
wyznacz część rzeczywistą i część urojoną funkcji:
wyznacz część rzeczywistą i część urojoną funkcji:
wyznacz część rzeczywistą i część urojoną funkcji:
rozwiąż równanie ze zmienną zespoloną:
rozwiąż równanie ze zmienną zespoloną:
rozwiąż równanie ze zmienną zespoloną:
rozwiąż równanie ze zmienną zespoloną:
rozwiąż równanie ze zmienną zespoloną:
wyznaczyć funkcję odwrotną do podanej:
wyznaczyć funkcję odwrotną do podanej:
wyznaczyć funkcję odwrotną do podanej:
rozwiąż równanie:
rozwiąż równanie:

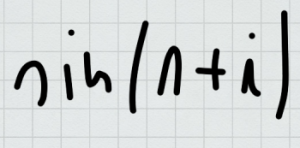
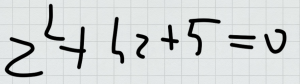
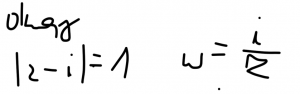
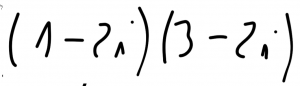
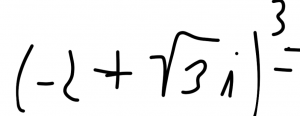
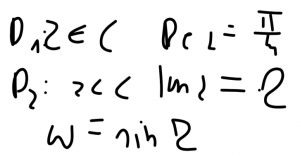
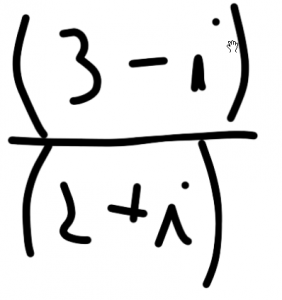
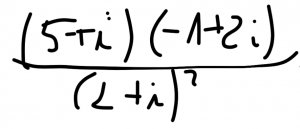
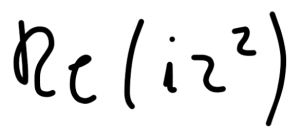 rozwiązanie
rozwiązanie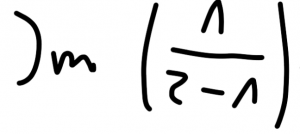


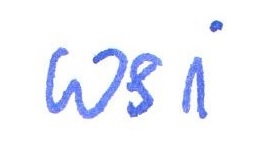 rozwiązanie
rozwiązanie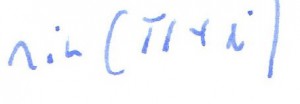
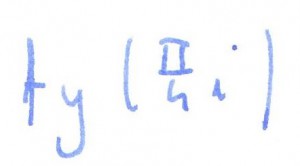
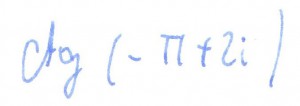
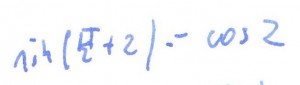
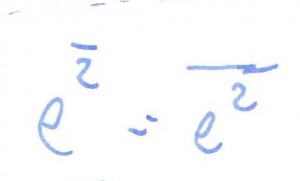

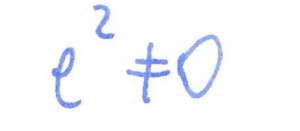
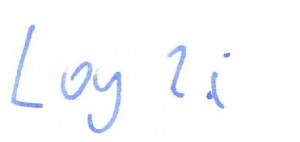 rozwiązanie
rozwiązanie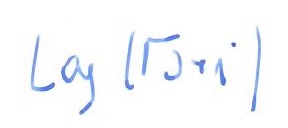
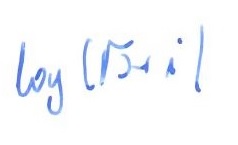
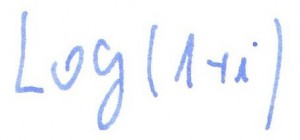 rozwiązanie
rozwiązanie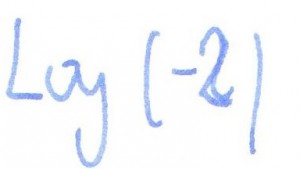
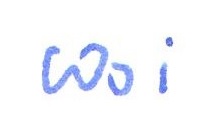

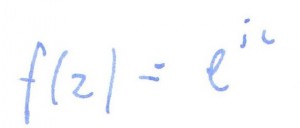

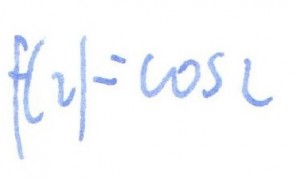
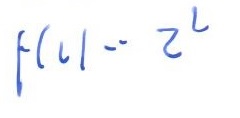
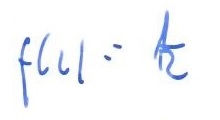
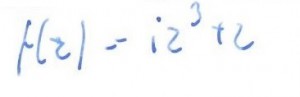
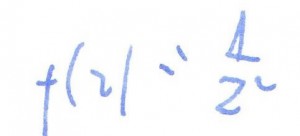
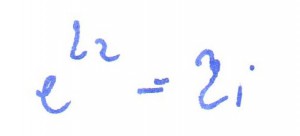

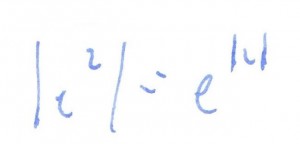

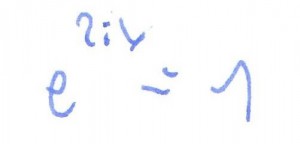
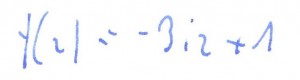

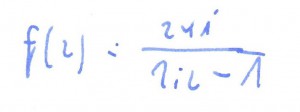
 rozwiązanie
rozwiązanie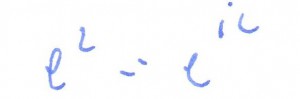
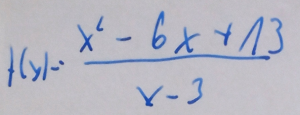 rozwiązanie
rozwiązanie